心理学などで3水準以上のグループの平均値を比較する際には分散分析と呼ばれる手法が用いられます。Rでは、デフォルトの状態であればaov関数(aov())を使うことで分散分析を行うことができます。
ただし、分散分析には平方和の計算の仕方の観点からいくつか種類があり、aov関数はそのうちのType Ⅰの平方和に基づいたもので,分析データによってはこの分散分析は適切でない場合もあるそうなので注意が必要です。
そこで、今回はTypeⅠとTypeⅡの平方和の2種類の分散分析をRで行う方法について触れます,
TypeⅠの平方和による分散分析をRで行う方法
TypeⅠの平方和による分散分析はaov()という関数を使います。
Rだとデフォルトの関数として最初から入っているので,パッケージのインストールなどをしなくてもはじめから使用可能です。
TypeⅠの平方和に基づく分散分析はバランスデザインデータで用いることが前提
TypeⅠの平方和に基づく分散分析は基本的にバランスデザインデータ(全ての条件におけるデータ数が一致している)ということが前提のようです。
そのため,参加者間要因が含まれている場合,各水準の人数が等しければ使用可能ということになります。
TypeⅠの平方和に基づく分散分析のやり方
具体的にRでTypeⅠの平方和に基づく分散分析のやり方を説明します。
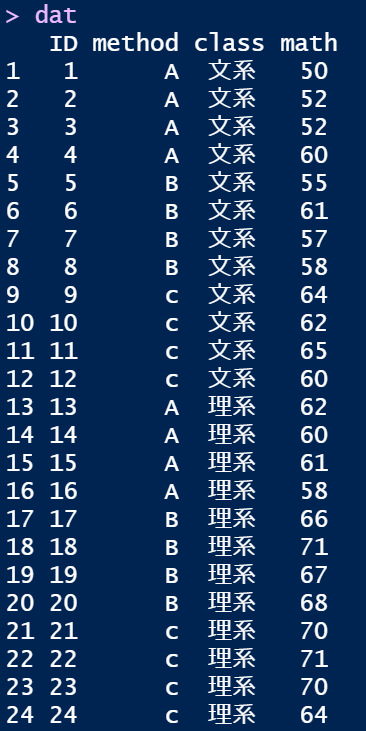
例として,教授法(A,B,C)×クラス(文系,理系)の各群4名ずつ(バランスデータ)の数学の成績という架空のデータをdatに用意しました。
ID<-c(1:24)
それっぽいデータですが,架空のデータです。
method<-rep(c(“A”,”B”,”c”),each=4,2)
class<-rep(c(“文系”,”理系”),each=12)
math<-c(50,52,52,60,55,61,57,58,64,62,65,60,62,60,61,58,66,71,67,68,70,71,70,64)
dat<-data.frame(ID,method,class,math)
実行すると,このようなデータが出来上がります(それっぽいデータですが,もちろん架空のデータです)。
aov関数は以下のように入力します。
summary(aov(従属変数~独立変数1*独立変数2) )
アスタリスク(*)を独立変数の間に入れることで,2つの変数の主効果と交互作用が出力されるようになります。
今回の例であれば,以下のように出力されます。
> summary(aov(dat$math~dat$method*dat$class))
Df Sum Sq Mean Sq F value Pr(>F)
dat$method 2 328.1 164.0 20.224 2.49e-05 ***
dat$class 1 352.7 352.7 43.479 3.42e-06 ***
dat$method:dat$class 2 20.6 10.3 1.269 0.305
Residuals 18 146.0 8.1
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
教授法と,クラスそれぞれで主効果が有意で,交互作用は有意ではないという結果が出ています。
注意点として,TypeⅠ平方和に基づくaov()で分散分析を行うと,要因の投入順序によって結果が変わってしまうようです。
実際に,先ほどのデータのID24番を除外したデータ(教授法C×クラス理系だけ3名のアンバランスデザイン)で分散分析を行うと以下のように要因の投入順序によって結果が変わってしまいます。
dat2<-dat[c(1:23),] # datのID23番までを使用(24番を除外)
> summary(aov(dat2$math~dat2$class*dat2$method))
Df Sum Sq Mean Sq F value Pr(>F)
dat2$class 1 350.8 350.8 51.447 1.56e-06 ***
dat2$method 2 362.5 181.2 26.579 5.85e-06 ***
dat2$class:dat2$method 2 13.3 6.6 0.972 0.398
Residuals 17 115.9 6.8
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1> summary(aov(dat2$math~dat2$method*dat2$class))
Df Sum Sq Mean Sq F value Pr(>F)
dat2$method 2 326.7 163.3 23.955 1.13e-05 ***
dat2$class 1 386.6 386.6 56.694 8.25e-07 ***
dat2$method:dat2$class 2 13.3 6.6 0.972 0.398
Residuals 17 115.9 6.8
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
平方和が異なれば当然,その後のF値やP値も変わってしまいます。
そのため,aov()で行う分散分析はバランスデザインでのみ利用できると覚えておくと良いと思います。
(なお,バランスデザインデータの場合は,投入順序を入れ替えても結果は変わりません)
TypeⅡの平方和に基づく分散分析のやり方
TypeⅡの平方和に基づく分散分析は,”car”というパッケージをインストールした後に使えるようになるAnova()を使います。
install.packages(“car”)
Anova()は,aov()を囲むようにして使いますが,式はTypeⅠの時と同じです。
summary(aov())がAnova(aov())に替わったというようなイメージです。
library(car)
Anova(aov(dat$math~dat$method*dat$class))
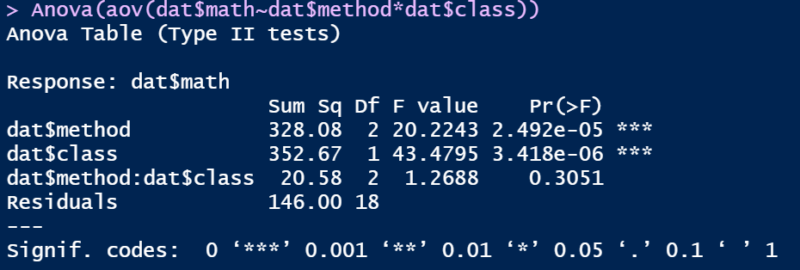
バランスデザインでの出力結果は以下のようになります。
TypeⅠのバランスデータのときと一致しています。
また,アンバランスデザインの場合(dat2)において,TypeⅡの場合は要因の投入順序を入れ替えても結果は同じです
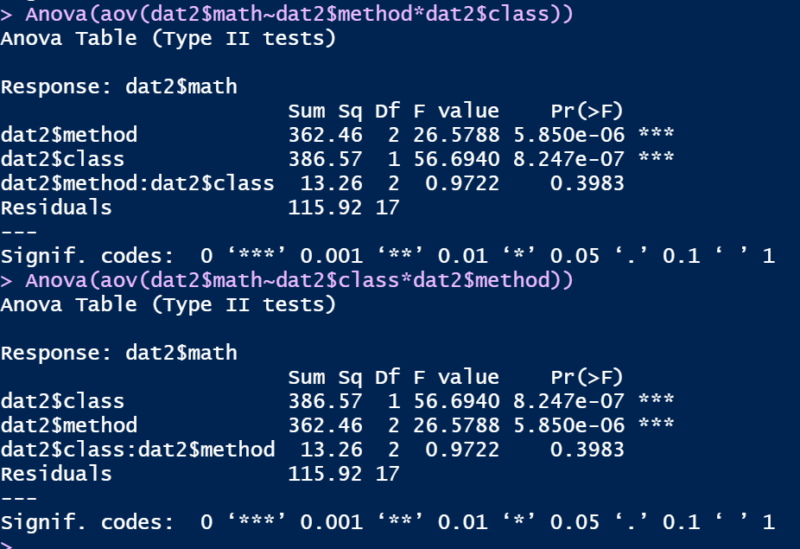
結果が要因の投入順序に左右されないという理由からも,アンバランスデザインの場合は,TypeⅡのほうが良い。
まとめ
この記事ではRで分散分析を行う方法について、平方和のtype別に2種類紹介しました。
typeⅠ平方和の場合はsummary (aov () )を使う
typeⅡ平方和の場合はcarパッケージをインストールして,Anova(aov())を使う
ただし,アンバランスデザインのときには,
typeⅠ平方和の場合,要因の投入順序によって結果が異なる
typeⅡ平方和の場合,要因の投入順序によって結果は異ならない
バランスデザインのときは,
typeⅠ平方和とtypeⅡ平方和の分散分析の結果は一致する
上記のことを踏まえると基本的にはtypeⅡ平方和の分散分析の方を使用するのが良さそうな気がします。
なお,他にもTypeⅢやTypeⅣといったものもあるらしいです。
TypeⅢはSPSSで分散分析するときのデフォルトの計算方法で,Anova()にオプションすれば指定できるため紹介したかったのですが,TypeⅡと何が違うのかとか使い分けとかよくわかっていないので勉強します。
参考図書
山田・村井・杉澤(2015)『Rによる心理データ解析』ナカニシヤ出版