重回帰分析を行ったとき、論文では標準偏回帰係数(β)の記載が求められることが多いと思います。
Rで重回帰分析を行うこと自体はlm関数を使って実施すると思いますが、標準化を行っていないデータセットで重回帰分析を行った場合は偏回帰係数(B)の値しか出力されません。
そのため、偏回帰係数を取り出すためには、標準化したデータセットを用いてlm関数を実行することで出力することができます。
出力された偏回帰係数の値が標準偏回帰係数を示します。
※重回帰分析の行い方は以下の記事をご参照ください。
ただ、この方法で実施した分析について、確認のためSPSSで実施した際に、なぜか偏回帰係数だけが一致しないというケースがありました。色々と考えてみたところ、原因がわかり、注意すべき点が1点あったので備忘録として残しておきます。
データセットの標準化は分析で使用するデータと一致させる
まず、標準化とは、平均やばらつきが異なる各変数について、平均を0、標準偏差を1に変換することです。
標準化を行うことで得点のばらつきが異なる複数の科目を比較することができます(大学受験で使われる偏差値が有名な例です)。
Rでデータセットを標準化する際には、scale関数を用いることで簡単にできるのですが、注意すべき点は、データセットの標準化は、「重回帰分析を行うデータ」を使って標準化を行わないといけないということです。
「重回帰分析を行うデータ」というのは独立変数(説明変数)として投入しているデータのことです。
Rで重回帰分析を行う際、独立変数に投入されている変数のうち、どれか1つでも欠損があるデータは、そのデータをまるまる一行除いて分析を行います。
そのため、例えば、以下のデータセットの場合、重回帰分析で使用されるデータとしては、C・D・Eの3つの物件が除かれてしまいます。
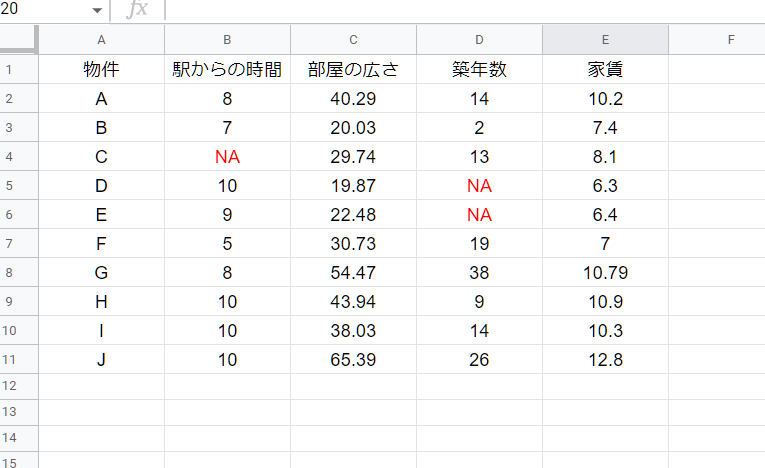
しかし、scale関数で標準化を行うと、「駅からの時間」の変数では、物件Cだけを除いた駅からの時間の平均と標準偏差をもとにした標準化得点が、「築年数」については物件DとEだけを除いた駅からの時間の標準化得点が出力されます。
そのため、重回帰分析で使用される物件のデータ(C・D・Eを除く変数)とは異なるデータ(駅からの時間ではDとEが入ってしまってるなど)を使って標準化得点が各物件について出力されてしまうことになり、誤った結果になってしまいます。
そのため、重回帰分析で使用するデータだけを残した状態にした後に標準化を行う必要があります。
欠損値が1つでもあるデータを除外する(リストワイズ除去)
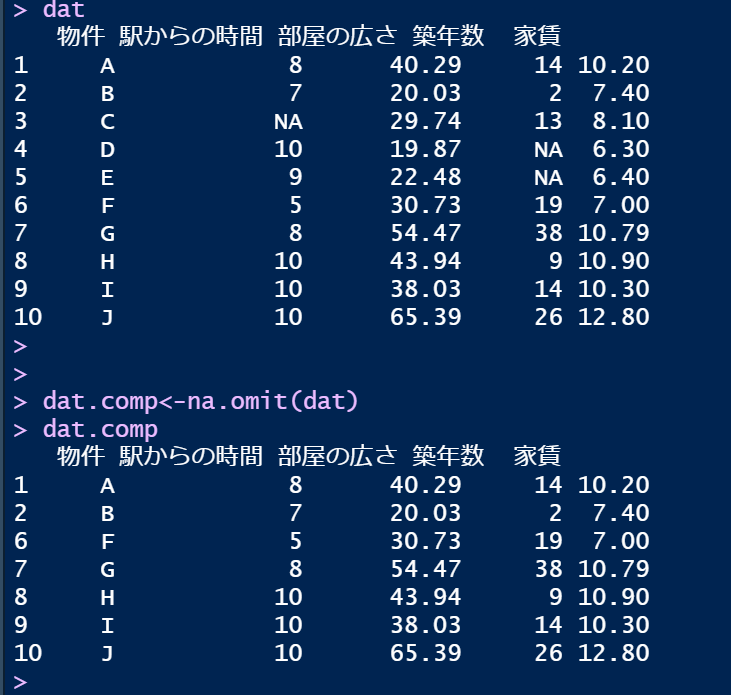
欠損値が1つでもあるデータ、上記であれば、物件C・D・Eを除くためには、na.omit関数を使います。
na.omit(データ名)で、欠損(NA)が1つでもあるデータを1行まるまる削除できます(リストワイズ除去)。
以下では、上記のデータを格納したdatに対してna.omitを行って完全なデータだけを残しています。
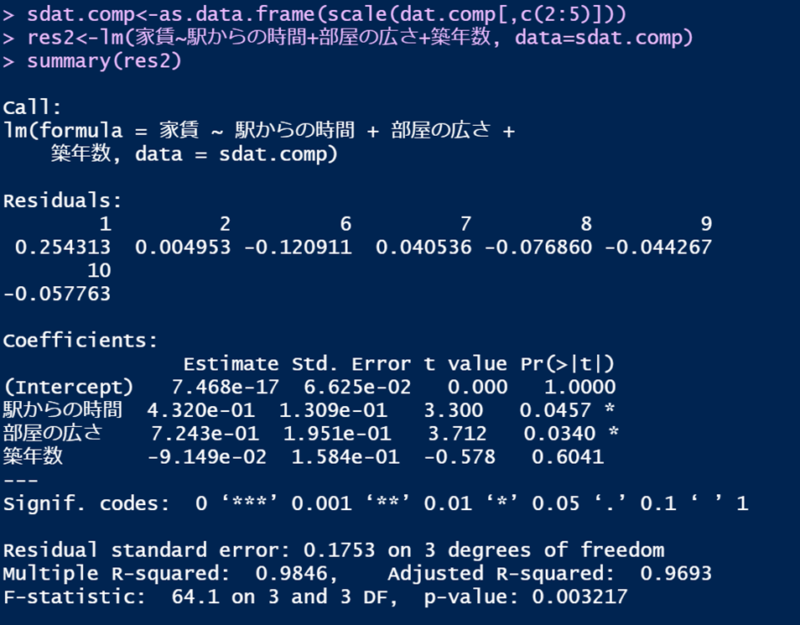
このように、重回帰分析にて実際に使用されるデータのみを残したうえで標準化を行えば、正しい結果が出力されます。
(省略しますが、回帰係数、t値、p値、R2乗の値など、標準化前の結果とも、SPSSでの結果とも一致します)
標準化偏回帰係数が正しく出力されていないときの見分け方
標準化がうまくできていない場合、今回の場合であれば、除外すべきデータが除外されていない状態で回帰係数が計算されていることを見分ける方法としては、切片の値を見るとよいです。
というのも、標準化を行った場合、切片は0になります。
(標準化前の切片は、独立変数の値がすべて0のときの値になるので、特定の値になることが決まっているわけではありません。)
上記の分析結果では、7.468 e-17となっており、限りなく0に近いです。(e-17は10のマイナス17乗です)
ちなみにですが、0になることがわかっているからか、SPSSではそもそも切片の値は出力されないようです。
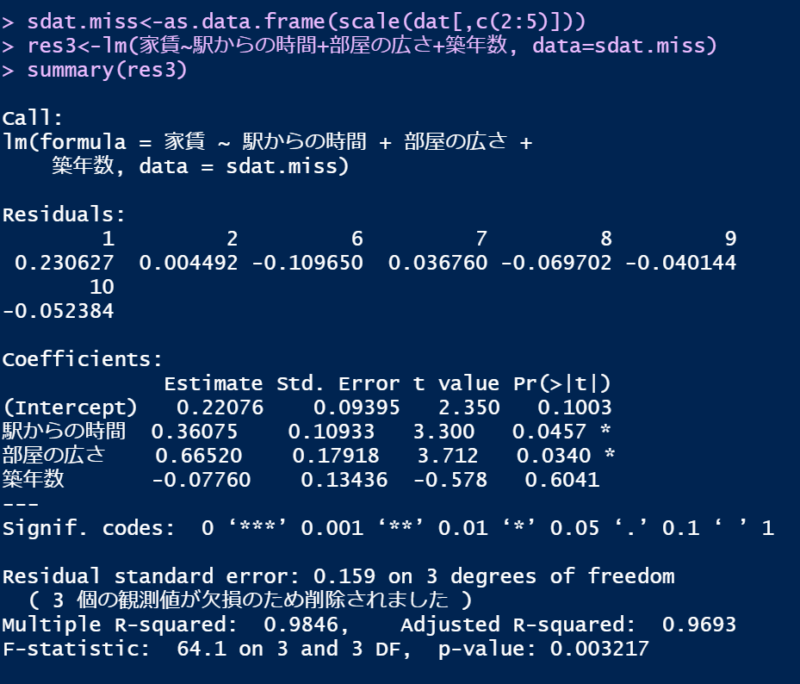
もし、標準化がうまくいっていない場合は以下のように、切片が0(に近い値)以外になっていることが多いです。
また、分析結果の下部に”〇個の観測値が欠損のため削除されました”と出ており、欠損値を除外した旨が記載されています。この場合、重回帰分析で使用しているデータが正しく標準化されていない可能性があるので注意が必要です。
p値は一致していて回帰係数(estimate)だけが異なり、そのまま結果を報告すると誤った標準化偏回帰係数を出してしまうことになるので注意が必要です。
まとめ
重回帰分析で標準化偏回帰係数を出す際には、scale関数で標準化させれば結果が出力されると説明されることが多いです。
しかし、実データでは欠損値も多いこともあり、そのため標準化したつもりでも標準化できていないことがあるかもしれないので注意が必要です。
もし、別ソフトと比較したときに結果が一致しない場合は、上記の可能性を検討してみるとよいかもしれません。
また、上記の方法以外にも出力された偏回帰係数と従属変数の標準偏差と独立変数の標準偏差を使って標準偏回帰係数を計算することも可能ですので、出力結果があっているかどうかを調べる際に確認してもよいと思います。


